TRYOUT
DOWNLOAD
PLUGINS
Ableton M4L-Plugins & Howto:
SRR-LFO SRR-MIDI SRR-CV
or: @maxforlive.com
CODE
https://github.com/steffenkrebber/sinusoidalrunrhythm
TEXT AUF DEUTSCH
Einführung
INTRODUCTION
At approximately 16 events per second, humans have an auditory and visual threshold between distinguishable individual events and the perception of flow. Visually, this threshold is the transition from single images to the continuous flow of a film, and auditorily it is the transition from rhythm to frequency. This transition is fraught with conceptual fuzziness. If, for example, one slows down a flute tone to a frequency that is heard as rhythm, one can only see the rhythm as a membrane movement of the loudspeaker and no longer hear the tone. Conversely, the special characteristics of an accelerated rhythm’s waveform result in timbre. These inaudible rhythms can become audible by using them as amplitude envelopes – as low frequency oscillators (LFO) often used in electronic music. If one adds up in-phase cosine functions in integer ratios – which are pure intervals in the audible range – these also entail special characteristics in the form of rhythms: they are temporally shifted in their maxima compared to corresponding notated, discrete rhythms, and are thereby something fundamentally different from polyrhythms in the same ratio a:b (→ Fig. 1). In addition, the rhythms have volume weightings between their maxima. ¹

This is interesting and relevant for music because the interplay of the deviations in time and volume feature a physicality that is not present in discretely controlled rhythms. In literature, depending on the milieu and context, this phenomenon is commonly referred to as groove, timing, agogic, phrasing, or interpretation – to name just a few terms. They are the flipside of a European written tradition whose theory of rhythm discriminates between an ideal, discrete, objective realm – how rhythm is (written) – and an individual, subjective, interpretive realm of how it actually appears in the world. This subobjective view also splits into an internal, subjective perception or conception of a rhythm and its external appearance or performance. The phenomenon of sinusoidal run rhythms can liberate the notion of rhythm from this dualism of objective-theoretical and subjective-individual-physical. It reveals a concept of rhythm as an “intra-action”² in human, instrument, computer, in the entanglement of imagined and sounding vibration.
“sinusoidal run rhythm” proposes a definition of rhythm as a wave. It does not conceive of time as discrete subdivisions, but makes it continuously quantifiable. Concurrently, through the aesthetics of wave additions, it does not present physicality as a merely subjective concept and thus liberates it from mystification.
Traditional European rhythmic theory thinks in terms of allegorical weight, i.e., heavy and light time. Because of the attractive proximity to physicality and dance, the terms gravity and also gravitational wave remain in the orbit of the sinusoidal run rhythm, though the allegory aims at cycles of time whose rotation is subject to varying degrees of attention. Less allegorically represented, it is about an attention-time bent by waves. Or: in the entanglement of felt and quantified time, rhythm becomes graspable as a stretching of attentional time. Such a theory is not to be understood in purely linguistic terms, but also aurally, informatically and visually. It entangles the areas of analysis, genesis, and interpretation, and offers significant possibilities in collaboration with the disciplines of music theory, musicology, interpretation, composition, computer music, and sound art:
1
Models of rhythmic gravity on both sides of the beat, which in many cases give more convincing explanations and applications than a discrete view. Especially in terms of what rhythmically belongs (is joined) together, they open up a more intuitive understanding than the discrete division of the European tradition of notation. The product of the curve value and the energy value of a sound file results in a curve, whose integral can be used to calculate the center of gravity of the respective beat or wave crest. This is most clearly illustrated in polar notation by imagining the area of the integral as a disk to be balanced. This is a promising approach with diverse applications for music theory analysis as well as for psychoacoustics.
2
Fitting models for common so-called “interpretation” of rhythm. A simple example is the phrasing of a waltz, which can be modeled with the ratio 1:3 (→ Fig. 2) and resulting deviations.
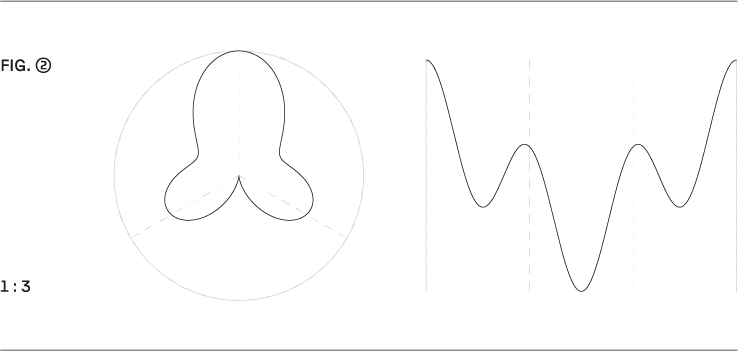
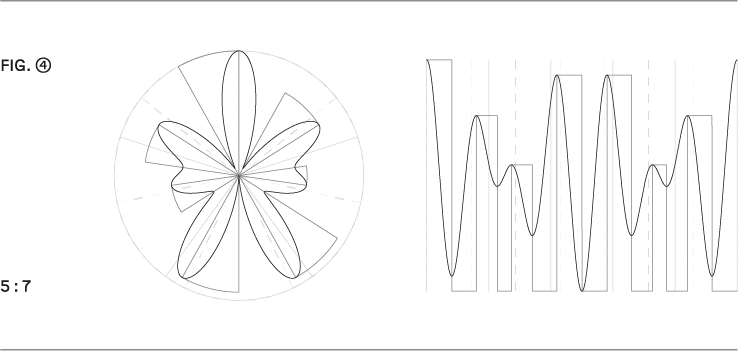
Such time deviations generated from rhythmic gravity are also applicable and intuitively comprehensible in more complicated ratios, for example at 5:7 (→ Fig. 3), which could be a model of a sub-Saharan clave with twelve subdivisions.

3
The genesis of music and sound art offers numerous fields of application. The appeal and relevance lie in the physicality of a non-discrete division of time. In my own experience, the simultaneity of different envelopes and their applications as complementary rhythms shifted by 180 degrees – for example, distributed over two loudspeakers – were productive. In particular, the “rediscretization” of the curves is interesting as a modulation source in this context, where at the high point the respective eigenvalue is held until the next low point and a pause occurs from the low point to the next high point (→ Fig. 4). Longer sequences are advisable with common subdivisions of, for example, 32, 64 or 128 in combination with some slower partials if one wants to alter them with the specific physicality of spectral rhythms.
–
The number of completely reduced ratios of two partial frequencies up to a specified maximum frequency corresponds to the number of Farey fractions which can be calculated by evaluating the Euler phi function. Combinations are counted, which are called “prime ratios” here. Musically speaking, these are pure intervals whose octave transpositions are not taken into account. With three partial frequencies, the number of prime ratios corresponds to the so-called “coprime triples.” ³
The curves are all symmetrical at 180 degrees. Curves composed purely of odd ratios are additionally symmetrical at the x-axis and then phase shifted by half. For the rediscretized graphs, this results in the durations of the “notes” and “pauses” of the first half being repeated backwards in the second half, with “notes” and “pauses” reversed.
With the accompanying website, LFOs can be generated and used with Ableton plugins as a modulation source or MIDI transformer. An animation of the polar plots illustrates their development with increasingly higher partial frequencies. (link coming soon)
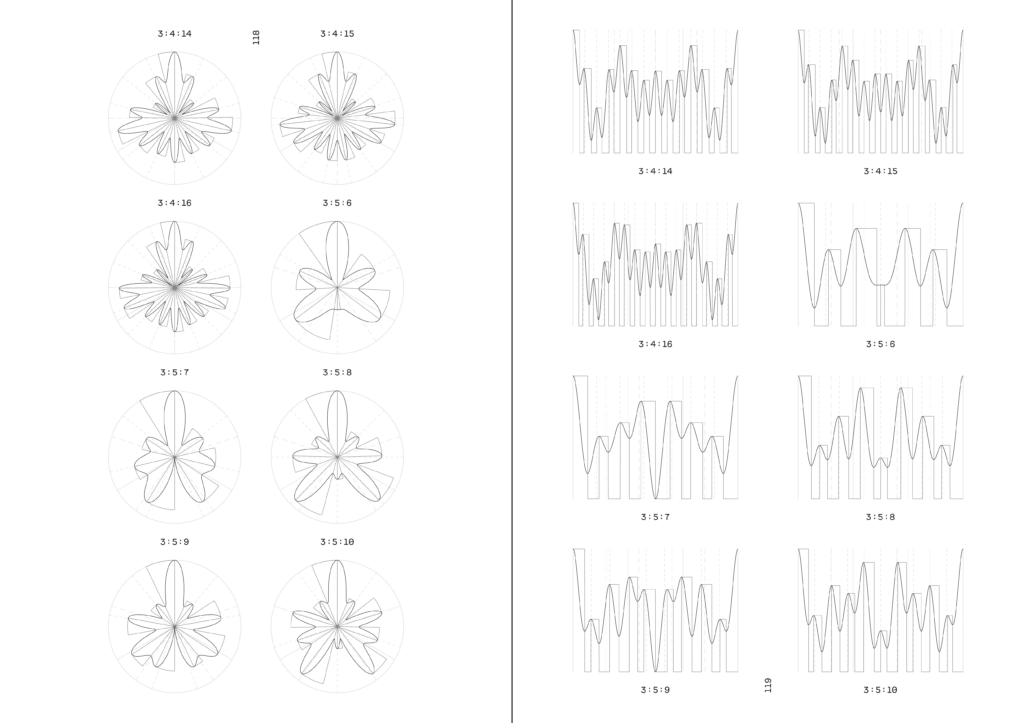
The book maps all prime ratios with two partial frequencies and all prime ratios with three partial frequencies up to 16. In addition, there are selected prime ratios with four partial frequencies up to 32. All figures also show the rediscretized representation. For each ratio there is a linear and a polar representation, which mathematically rotates time counterclockwise. The book is limited to in-phase ratios. The publications following this volume will be devoted in particular to phase shifts whose exact length is derived from a two-prime ratio.
In addition to the immediate visual appeal of the figures, the book, which is modeled on natural handbooks for species identification from the late 19th century, offers the opportunity to follow their course of change and to look for special specimens – for example, those that have fewer high points than the frequency of the highest partial. Listening to the models with the help of the web page or plug-in offers the possibility of finding existing applications for the models and discovering that some inconspicuous images sound surprisingly interesting. Ideally, the volume serves as an introduction to scientific or artistic work in an expanded rhythmic space that quickly develops a gravitational pull and momentum of its own.
¹ Why these points have been overlooked until now, even though the possibility of precise control of phase equality arose with the advent of computers, is not clear to me.
² Barad, Karen. 2007. Meeting the Universe Halfway : Quantum Physics and the Entanglement of Matter and Meaning. Durham, N.C. ; London: Duke University Press.
³ OEIS Foundation Inc. (2023), Entry A005728 and Entry A015616 in The On-Line Encyclopedia of Integer Sequences. https://oeis.org/A005728. https://oeis.org/A015616
EINFÜHRUNG
Bei ungefähr 16 Ereignissen pro Sekunde liegt beim Menschen eine auditive und visuelle Wahrnehmungsschwelle zwischen unterscheidbaren Einzelereignissen und einem Wahrnehmungsfluss. Visuell ist diese Schwelle der Übergang von Einzelbildern zum kontinuierlichen Ablauf eines Films, auditiv der Übergang von Rhythmus zu Frequenz. Dieser Übergang ist mit einer konzeptuellen Unschärfe behaftet. Verlangsamt man beispielsweise einen Flötenton auf eine als Rhythmus hörbare Frequenz, kann man den Rhythmus nur noch als Membranbewegung des Lautsprechers sehen und nicht mehr hören. Andersherum bringt ein beschleunigter Rhythmus die Spezifika seiner Signalform als Klangfarbe mit. Die unhörbaren Rhythmen können hörbar werden, indem sie als Amplitudenhüllkurve benutzt werden – als “Low Frequency Oscillator” (LFO) in der elektronischen Musik mit einiger Patina behaftet. Addiert man in ganzzahligen Verhältnissen stehende, phasengleiche Cosinusfunktionen – im hörbaren Bereich reine Intervalle – bringen diese ebensolche besonderen Spezifika in Form von Rhythmen mit: Sie sind in den Hochpunkten zeitlich verschoben zu entsprechenden notierten, diskreten Rhythmen und dabei etwas grundsätzlich anderes als Polyrhythmen im selben Verhältnis a:b (→ Fig. 1). Zudem weisen die Rhythmen Lautstärkegewichtungen zwischen den Hochpunkten auf. ¹

Das ist interessant und relevant für Musik, weil die Abweichungen in Zeit und Lautstärke im Zusammenspiel eine Körperlichkeit mit sich bringen, die bei diskret gesteuerten Rhythmen in dieser Form nicht vorhanden ist. In der Literatur wird dieses Phänomen je nach Milieu und Kontext gemeinhin als Groove, Timing, Agogik, Phrasierung oder Interpretation bezeichnet – um nur einige Begriffe zu nennen. Sie sind die andere Seite einer europäischen Schrifttradition, deren Rhythmustheorie in einen idealen, diskreten, objektiven Bereich – wie der Rhythmus (geschrieben) ist – und einen individuellen, subjektiven, interpretatorischen Bereich des realen Auftretens in der Welt trennt. Dieser subobjektive Blick spaltet auch in eine innere, subjektive Wahrnehmung oder Vorstellung von einem Rhythmus und dessen äußeren Erscheinen oder Ausagieren. Das Phänomen der sinusoidal run rhythms kann den Rhythmusbegriff aus diesem Dualismus von objektiv-theoretisch und subjektiv-individuell-körperlich befreien. Es eröffnet einen Rhythmusbegriff in einer “Intraaktion” ² in Mensch, Instrument, Computer, in Verschränkung von vorgestellter und klingender Schwingung.
SINUSOIDAL RUN RHYTHM schlägt eine Definition von Rhythmus als Welle vor. Sie fasst Zeit nicht diskret unterteilend, sondern macht sie kontinuierlich quantifizierbar. Dabei bringt sie durch die Ästhetik der Wellenadditionen Körperlichkeit nicht als nur subjektiven Begriff mit und befreit ihn so aus einer Mystifizierung.
Die traditionelle europäische Rhytmustheorie denkt mit einer Gewichtsallegorie, im Sinne von schwerer und leichter Zeit. Wegen der attraktiven Nähe zu Körperlichkeit und Tanz bleiben die Begriffe Gravitation und auch Gravitationswelle in der Umlaufbahn der neuen Theorie, wobei die Allegorie wohlgemerkt auf Zeitzyklen, deren Rotation unterschiedlich starker Aufmerksamkeit ausgesetzt ist, zielt. Weniger allegorisch gesprochen, handelt es sich um eine durch Wellen gekrümmte Aufmerksamkeitszeit. Oder: In der Verschränkung von gefühlter und quantifizierter Zeit wird Rhythmus als Dehnung von Aufmerksamkeitszeit fassbar. Eine solche Theorie versteht sich explizit nicht rein sprachschriftlich, sondern auch auditiv, informatisch und visuell. Sie verschränkt in den Bereichen Analyse, Genese und Interpretation den Raum und bietet in Zusammenarbeit mit den Disziplinen Musiktheorie, Musikwissenschaft, Interpretation, Komposition, Computermusik und Klangkunst vieles an:
1
Modelle von rhythmischer Gravitation beidseits eines klassischen „Zählzeitpunktes“, die in vielen Beispielen überzeugendere Erklärungen und Anwendungen bieten als eine diskrete Betrachtung. Gerade in Bezug darauf, was rhythmisch zusammen gehört (wird), eröffnen sie ein intuitiveres Verständnis als die diskrete Aufteilung, die aus einer europäischen Schrifttradition geboren wurde. Das Produkt des Kurvenwerts und des Energiewerts eines Soundfiles ergibt eine Kurve, mittels deren Integral sich der Schwerpunkt des jeweiligen Taktes oder Wellenbergs errechnen lässt. Am anschaulichsten wird dies in Polardarstellung, indem man sich die Fläche des Integrals als zu balancierende Scheibe vorstellt. Das ist sowohl für musiktheoretische Analyse als auch für Psychoakustik ein vielversprechender Ansatz mit vielfältigen Anwendungsmöglichkeiten.
2
Passende Modelle für gängige sogenannte Interpretationen von Rhythmus. Ein einfaches Beispiel ist die Phrasierung eines Walzers, das man mit dem Verhältnis 1:3 (→ Fig. 2) und der damit verbundenen Abweichung gut nachbilden kann.
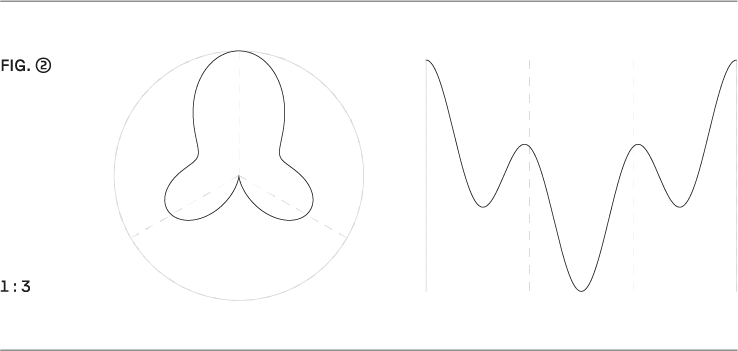
Solche aus rhythmischer Gravitation generierten Zeitabweichungen sind auch in komplizierteren Verhältnissen anwendbar und intuitiv nachvollziehbar. So zum Beispiel bei 5:7 (→ Fig. 3), das ein Modell einer subsaharischen Clave mit zwölf Unterteilungen sein könnte.

3
Vielfältige Anwendungsbereiche bietet die Genese von Musik und Klangkunst. Reiz und Relevanz liegen in der Körperlichkeit einer nicht diskreten Zeitaufteilung. In meinen eigenen Erfahrung waren unter anderem die Gleichzeitigkeit von verschiedenen Hüllkurven und deren Anwendungen und Eigenschaft als um 180 Grad verschobene Komplementärrhtyhmen – zum Beispiel auf zwei Lautsprecher verteilt – produktiv. Insbesondere die ‚Rediskretisierung‘ der Kurven, bei der am Hochpunkt der jeweilige Eigenwert bis zum nächsten Tiefpunkt gehalten und vom Tiefpunkt bis zum nächsten Hochpunkt eine Pause erklingt, sind in diesem Zusammenhang als Modulationsquelle interessant (→ Fig. 4). Längere Abläufe mit gängigen Unterteilungen zum Beispiel von 32, 64 oder 128 in Kombination mit einigen langsameren Teiltönen bieten sich an, wenn man ästhetisch an solche anknüpfen und mit der spezifischen Körperlichkeit der spektralen Rhythmen infizieren will.

–
Die Anzahl der vollständig gekürzten Verhältnisse von zwei Teilfrequenzen bis zu einer festgelegten Höchstfreuquenz entspricht der Anzahl von Farey-Brüchen, die mit Hilfe der Auswertung der Eulerschen Phi-Funktion berechnet werden kann. Es werden Kombinationen gezählt, die hier ‘Primverhältnisse’ genannt werden. Musikalisch gesprochen handelt es sich um reine Intervalle, deren Oktavierungen nicht berücksichtigt werden. Bei drei Teilfrequenzen entspricht die Anzahl der Primverhältnisse den sogenannten ‘coprime triples’ . ³
Mit der begleitenden Webseite lassen sich LFOs in Primverhältnissen herstellen und mit den Ableton-Plugins als Modulationsquelle oder MIDI-Transformer nutzen. Eine Animation der Polardarstellungen veranschaulicht ebendort deren Entwicklung mit zunehmend hohen Teilfrequenzen.
Das Buch bildet alle Primverhältnisse mit zwei Teilfrequenzen und drei Teilfrequenzen bis 16 ab. Dazu kommen ausgesuchte Primverhältnisse mit vier Teilfrequenzen. Alle Abbildungen zeigen auch die rediskretisierte Darstellung. Für jedes Verhältnis gibt es eine lineare und eine polare Darstellung, welche Zeit mathematisch positiv gegen den Uhrzeigersinn dreht. Das Buch beschränkt sich auf phasengleiche Verhältnisse. Die auf diesen Band folgenden Veröffentlichungen werden sich insbesondere den Phasenverschiebungen widmen, deren genaue Länge sich aus einem Zweier-Primverhältnis ableitet.
Das Buch, an Naturhandbücher zur Artenbestimmung des ausgehenden 19. Jahrhunderts angelehnt, bietet neben dem unmittelbaren visuellen Reiz der Figuren Gelegenheit, deren Änderungsverläufe mitzuverfolgen und dabei nach besonderen Exemplaren Ausschau zu halten – beispielsweise nach solchen, die weniger Hochpunkte haben als die Frequenz des höchsten Teiltones. Der hörende Abgleich mithilfe von Webseite oder Plugin birgt die Möglichkeit, schon vorhandene Anwendungen der Modelle zu finden und zu entdecken, dass manche unscheinbare Bilder überraschend interessant klingen. Idealerweise dient der Band als Einstieg in wissenschaftliche oder künstlerische Arbeit in einem erweiterten Rhythmusraum, der schnell einen Sog und eine Eigendynamik entwickelt.
1 Warum diese Punkte bisher übersehen wurden, obwohl die Möglichkeit einer genauen Kontrolle der Phasengleichheit mit Aufkommen der Computer entstand, ist mir nicht klar.
2 Karen Barad, Meeting the Universe Halfway. Quantum Physics and the Entanglement of Matter and Meaning, Durham, NC: Duke University Press, 2007
³ OEIS Foundation Inc. (2023), Entry A005728 and Entry A015616 in The On-Line Encyclopedia of Integer Sequences. https://oeis.org/A005728. https://oeis.org/A015616

gefördert von